Introduction
Pharmaceutical calculations serve as the backbone of pharmacy practice. Which ensures precise medication dosing, compounding and preparation. From converting units of weight and volume to calculating complex solutions and formulations, pharmaceutical calculations are essential for pharmacist. There are two-unit systems of weights and measures in pharmacy, one is imperial and another is metric. In this article we will see these two systems and calculations involving percentage solutions, allegations, proof spirit and isotonic solutions based on freezing point and molecular weight.
Imperial system
It is an old system of weights and measures. Weight is a measure of the gravitational force acting on a body and is directly proportional to its mass. The imperial system has two types, one is avoirdupois system and another is apothecaries system.
Avoirdupois System
Avoirdupois is the French word derived from the phrase, “avoir du pois” where, avoir means to have, du means of the and pois means weight. In the avoirdupois system the basic unit of weight is pound which is further divided into ounces. One pound is equivalent to 16 ounces. The avoirdupois system also includes larger and smaller units such as the ton (equal to 2000 pounds), the hundred weight (equal to 100 pound) and the grain (equal to 1/7000th of a pound).
1 ounce (oz) avoirdupois = 16th part of 1 pound
1 grain = 7000th part of 1 pound
Apothecaries system
In this system grain (gr) is taken as the standard of weight. The word apothecary is derived from Greek word apotheke means storing place. It includes a set of special weights known as troy weights or apothecaries. Weights are measured in grains, scruples, drams, ounces and pounds. Each unit have specific conversions.
1 grain = 1/7000 pound
1 scruple = 20 grains
1 dram = 3 scruples
1 ounce = 8 drams
1 pound = 12 ounces
60 grains = 1 dram
480 grains = 1 apothecaries or troy ounce
12 apothecaries = 1 troy pound or 5760 grains
Measurements of volumes
Imperial standard gallon is used as the standard. It is secondary standard related to the imperial standard pound. Therefore, it is called as derived standard. The gallon is defined as the volume occupied by 10 imperial standard pounds weight of distilled water weighed in air at 620F at 30 inches pressure. All other weights are called as derived weights.
1 gallon = 4 quart
1 quart = 2 pint
1 pint = 20 fluid ounce
1 fluid ounce = 8 fluid dram
1 fluid dram = 3 fluid scruple
1 fluid scruple = 20 minims
Metric system
The metric system is an international system of measurement used in most countries around the world. It is based on the units such as meter for length, kilogram for mass and litre for volume. It provides a standardized way to measure and communicate quantities, making it easier for people across different regions to understand and work with measurements consistently. In India, metric system is legalised by the act “The Standards of weights and measures Act 1976.”
Measures of weights (mass)
In metric system, standard for weight is kilogram. For measuring small quantities of a substance, there are several derived forms of kilogram are available. Like,
1 kilogram (kg) = 1000 grams (gm)
1 gram = 1000 milligrams (mg)
1 milligram = 1000 micrograms (mcg)
1 microgram = 1000 nanogram (ng)
Measures of capacity (volume)
Capacity refers to the maximum quantity of liquid or any pourable substance that a container can hold. It is often used interchangeably with the term volume. In the metric system, we use two primary units to express capacity. Litre (L) is the standard unit for measuring capacity. It represents the volume of liquid contained in a cubic decimetre (a cube with sides of 10 centimetres each). Millilitre (mL) is a smaller unit of capacity. One millilitre is equal to one-thousandth of a litre (1 mL = 0.001 L).
Measures of length
The meter (m) is the fundamental unit of length in the metric system. It represents distance or length. There are several secondary measures of length, derived from meter.
1 kilometre (km) = 1000 metrewhat
1 meter = 100 centimetre (cm)
1 centimetre = 10 millimetre (10mm)
Advantages of metric system
- Straightforward Conversions: The metric system allows for easy conversions between units by changing the decimal place value. Metric units increase or decrease in multiples of 10, making calculations straightforward.
- Consistency and Continuity: Nearly all countries use the metric system, ensuring global uniformity. Students, educators, and scientists can rely on the same system of measurement across disciplines.
- Easy Root Words and Terminology: Metric terminology is easier to learn because unit names share the same root word. For example, when measuring weight, the root word is “gram” and also Milligram (mg), centigram (cg), and kilogram (kg) all derive from “gram.” In contrast, the imperial system uses units that do not sound alike (e.g., ounces, pounds, tons).
- Avoids Errors: The metric system minimizes errors due to its logical structure. Using consistent prefixes (e.g., milli-, centi-, kilo-) ensures clarity. Arithmetic conversions are straightforward, reducing the risk of mistakes.
- Future-Proof: As science and technology advance, the metric system remains adaptable. It accommodates both very large and very small values with ease.
Allegation method of percentage calculations
The allegation method is a mathematical technique used in pharmacy and other fields to calculate the proportions of different components needed to create a mixture of a desired strength or concentration. It is particularly useful when compounding medications or adjusting existing solutions. Here’s how the allegation method works, along with an example.
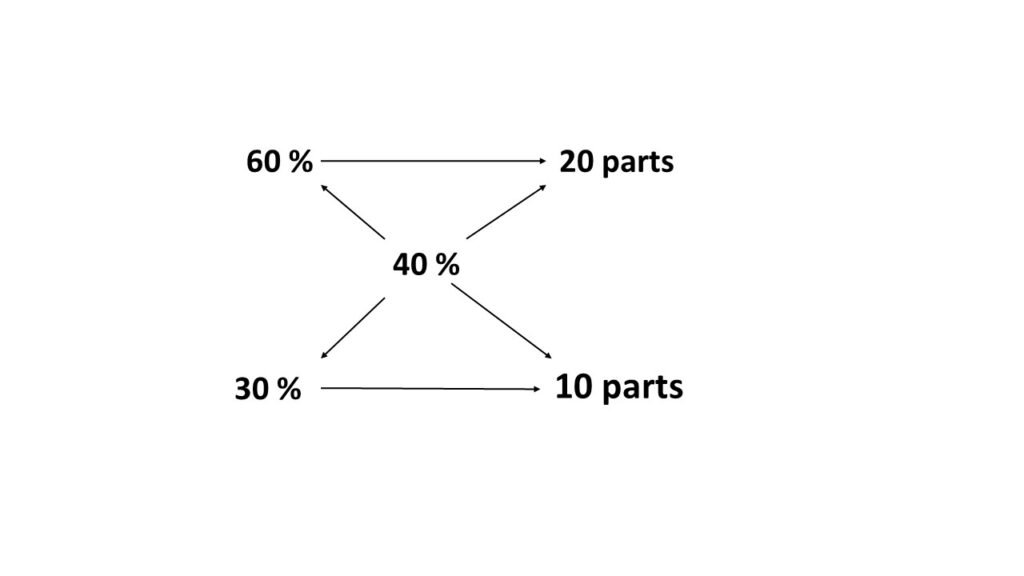
In what proportion should 60% solution to be mixed with 30% solution to obtain 40% solution?
Solution: We have two solutions in stock,
- 60% solution (stronger than needed)
- 30% solution (weaker than needed)
Lets, solve this problem using rectangle method of allegation. Here are the steps involved in the calculation.
- Put the known strengths on the left corner of the rectangle.
- Place the required strength at a point where the diagonals meet.
- Subtract the smaller figure from the bigger one on the same diagonal and place the figure on the other end of the diagonal.
- The figures so obtained represent the number of parts of strength of the solution to be mixed.
Percentage strength of a mixture
In such type of problems different volumes of different percentages are given and the final percentage strength of the final mixture is to be calculated.
Example: 20 gallons of 40%, 30 gallons of 60% and 40 gallons of 80% alcohols are mixed. Then what will be the percentage strength of final mixture?
Solution: First, multiply the volume by percentage,
(20X40) + (30X60) + (40X80) = 800 + 1800 + 3200 = 5800
Now, divide 5800 with total volume (20+30+40) = 90
Percentage strength of a mixture = 5800/90 = 64.44%
Hence, the final percentage strength of the alcohol solution will be 64.44%.
Specific gravity of a percentage solution
When solutions of different concentrations are mixed, their specific gravity can be calculated by following steps,
- Multiply the volume with the corresponding gravity of an individual solution.
- Add the volume of all liquids.
- Add all the products of multiplication.
- Then use the following formula.
Specific gravity = (sum of product of multiplication) / (sum of volumes)
Example: What is the resultant specific gravity of the final solution, if the following solutions are mixed?
100ml solution of 0.9 specific gravity
200ml solution of 1.0 specific gravity
300ml solution of 1.1 specific gravity
Solution
(100X0.9) + (200X1.0) + (300X1.1) = 90.0+22.0+330.0 = 620
We have total volume of 600ml. now using formula,
Specific gravity = (sum of product of multiplication) / (sum of volumes)
Specific gravity = 620 / 600 = 1.03
Hence, the specific gravity of the final solution will be 1.03
Proof spirit calculations
In pharmaceutical calculations, proof spirit is a term used to describe the strength of an alcohol solution. Proof spirit refers to an aqueous solution containing 57.1% v/v (volume/volume) of absolute alcohol. It is considered to be 100% Proof. The specific gravity of proof spirit at 15.5°C is approximately 0.9176. It contains 57.1% v/v of ethyl alcohol to 100 volumes of proof spirit.
To convert any percentage strength of alcohol to proof strength (P.S.), use the following formula.
P.S. = 1.753 × strength of alcohol in v/v % – 100
If the result is positive, it is known as overproof, if negative, it is underproof. The value 1.753 is obtained as follows,
57.1 volume of ethyl alcohol = 100ml of proof spirit
1 volume of ethyl alcohol = 100/57.1 = 1.753 volume of proof spirit.
Example1: What is the proof strength of 95% v/v alcohol?
Solution: By applying the formula,
P.S. = 1.753 × strength of alcohol in v/v % – 100
P.S. = 95 X 1.753 – 100
P.S. = 166.53 – 100
P.S. = +66.530 O.P.
Example2: Calculate the strength of 300 O.P and 400 U.P.
Solution
300 over proof = 100 + 30 = 130
400 under proof = 100 – 40 = 60
For 300 over proof,
Alcohol strength = (100+30)/1.753 = 130/1.753 = 74.15% v/v
For 400 under proof,
Alcohol strength = (100-40)/1.753 = 60/1.753 = 34.23% v/v
Isotonic solutions
The solutions which have same osmotic pressure or equal solute concentrations are called as isotonic solutions. The standard isotonic solution with blood plasma is 0.9% sodium chloride. Any concentration above this (0.9%) is considered as hypertonic solution and below this (0.9%) is considered as hypotonic solution.
Methods of adjustment of tonicity
There are four methods of tonicity adjustment.
- NaCl equivalent method
- Cryoscopic method (freezing point depression)
- Molecular concentration method
- White Vincent method
NaCl equivalent method
Sodium chloride equivalent (E) of drug means amount of sodium chloride equivalent to 1 gram of drug having same osmotic pressure as that of the drug.
E = (17 X Liso) / M
Where, Liso = freezing point depression of drug solution for showing isotonicity
M = molecular mass
After calculating E value, the percentage of sodium chloride require for adjusting tonicity can be calculated by following equation (valid for 100 ml),
PSA = 0.9 – (PSM E of drug)
Where, PSM = percentage strength of medicament
PSA = percentage of sodium chloride for adjustment of isotonicity
Cryoscopic method
In this method isotonic solution is prepared by using the freezing point depression method. The freezing point depression value (ΔTf) for isotonic solution is adjusted to -0.520C, which is ΔTf value of blood. Using this value isotonicity of the solution is achieved. If it is not possible to adjust the tonicity by changing drug concentration, then adjusting substance is added to achieve tonicity. The quantity of adjusting substance can be calculated as follows,
Total drug solution ΔTf = ΔTf of drug + ΔTf of adjusting substance
ΔTf for adjusting solution = w X a
Where w = weight of adjusting substance in grams per 100 ml
a = ΔTf of the adjusting substance (sodium chloride 0.58)
for an isotonic solution weight of the adjusting substance (w) is calculated as
-0.520C = d+wa (where d = x X ΔTf of 1% drug solution)
w = 0.52- d/a
w = 0.52- d/0.58
This equation is valid if 1% of drug solution is used. For any other given percentage strength of medicament (PSM), the modified equation is
w = [0.52- (PSM X d)]/0.58
if there are two or more substances are present, sum of their freezing point depression is considered.
Molecular concentration method
In this method molecular concentration of required solution is calculated by using following formula,
% w/v of adjusting substance required = 0.03M / N
Where,
M= gram molecular weight
N= number of ions into which the substance is ionised
Example: How to prepare isosmotic solution using dextrose. (molecular weight of dextrose = 180)
Solution: By using above formula,
% w/v of adjusting substance required = 0.03M / N
W = 0.03 X 180 = 5.4
Hence to prepare isosmotic solution of dextrose we need to mix 5.4gm of dextrose in water to produce 100ml solution.
White-Vincent method
White and Vincent developed a mathematical equation for calculating isotonicity. The equation is derived as,
To prepare 30 ml of 1% (w/v) solution of procaine hydrochloride isotonic with body fluid (0.3 gm),
V = weight of drug X E of drug
V = 0.3 X 0.21 =0.063 gm
The volume (V) of isotonic solution that can be prepared from 0.063 gm of NaCl is obtained by,
0.9 / 100 ml = 0.063 / V
V = 0.063 X 100 / 0.9 = 7 ml
Summary
The article covers various pharmaceutical calculations and methods including those used in the imperial and metric system, percentage calculations, allegation method, proof spirit and isotonicity adjustment methods. It provides insights into how these calculations and methods are applied in pharmacy practice to ensure accurate dosing and formulations.
For practice MCQ on above topic please visit: Practice MCQ For Government Exams » PHARMACAREERS
For more regular updates you can visit our social media accounts,
Instagram: Follow us
Facebook: Follow us
WhatsApp: Join us
Telegram: Join us

1 thought on “Pharmaceutical Calculations”